Download some benchmark road networks for Shortest Paths algorithms
Updated September 26, 2022 bugfix
The goal of this Python notebook is to download and prepare a suite of benchmark networks for some shortest path algorithms. We would like to experiment with some simple directed graphs with non-negative weights. We are specially interested in road networks.
The files are available on the Universita Di Roma website. It was created for the 9th DIMACS implementation challenge : Implementation Challenge about Shortest Paths. This challenge dates back to 2006, but the files are still there. Here is the download web page : http://www.diag.uniroma1.it//challenge9/download.shtml
The networks correspond to different parts of the USA road network, with various region sizes. Here are the different network names, from smaller to larger:
- NY : New York
- BAY : Bay area
- COL : Colorado
- FLA : Florida
- NW : North West
- NE : North East
- CAL : Califorinia
- LKS : Great Lakes
- E : Eastern region
- W : Western region
- CTR : Central region
- USA : contiguous United States
There is an interesting warning on the download page :
Known issues: the data has numerous errors, in particular gaps in major highways and bridges. This may result in routes that are very different from real-life ones. One should take this into consideration when experimenting with the data.
This does not really matter to us because the plan is to implement a shortest path algorithm in Python/Cython and to compare various implementations, but not to find realistic routes.
The networks are available as compressed text files. So here are the very simple steps followed in this notebook:
- create a folder structure
- download the compressed network files
- uncompress them with gzip
- Create a function to load the edges into a Pandas dataframe
- Create a function to load the node coordinates into a Pandas dataframe
- Save the networks into parquet files
- Query the parquet files with DuckDB
- Plot the networks with Datashader
Imports
import gzip
import os
import shutil
import datashader as ds
from datashader.bundling import connect_edges
import datashader.transfer_functions as tf
import duckdb
import geopandas as gpd
import numpy as np
import pandas as pd
import wget
DATA_DIR_ROOT_PATH = "/home/francois/Data/Disk_1/" # root data dir
Package versions:
Python : 3.10.6
datashader: 0.14.2
duckdb : 0.5.0
geopandas : 0.11.1
numpy : 1.22.4
pandas : 1.4.4
pyarrow : 9.0.0
pygeos : 0.13
wget : 3.2
Create a folder structure
We start by creating a main directory DIMACS_road_networks, and then one directory per network.
data_dir_path = os.path.join(DATA_DIR_ROOT_PATH, "DIMACS_road_networks")
if not os.path.exists(data_dir_path):
os.makedirs(data_dir_path)
names = [
"NY",
"BAY",
"COL",
"FLA",
"NW",
"NE",
"CAL",
"LKS",
"E",
"W",
"CTR",
"USA",
]
network_dir_paths = {}
for name in names:
network_dir_path = os.path.join(data_dir_path, name)
if not os.path.exists(network_dir_path):
os.makedirs(network_dir_path)
network_dir_paths[name] = network_dir_path
!tree -d {data_dir_path}
/home/francois/Data/Disk_1/DIMACS_road_networks
├── BAY
├── CAL
├── COL
├── CTR
├── E
├── FLA
├── LKS
├── NE
├── NW
├── NY
├── USA
└── W
12 directories
Download the compressed network files
Three types of files are available from the DIMACS challenge web site:
- Distance graph: edges with distance weight
- Travel time graph: edges with travel time weight
- Coordinates: node coordinates (latitude, longitude)
However, we are only going to download the coordinates and travel time graph files in the present notebook. We only require one type of edge weight in order run shortest path algorithms. So between weight=distance or weight=travel_time, we chose the latter.
The file URL has a neat pattern.
- travel time graph :
http://www.diag.uniroma1.it//challenge9/data/USA-road-t/USA-road-t.XXX.gr.gz - coordinates :
http://www.diag.uniroma1.it//challenge9/data/USA-road-d/USA-road-d.XXX.co.gz
where XXX is the network name. So we download each of these files with wget and save them in the respective network folder.
travel_time_graph_file_paths = {}
coordinates_file_paths = {}
for name in names:
# travel time graph
travel_time_graph_url = f"http://www.diag.uniroma1.it//challenge9/data/USA-road-t/USA-road-t.{name}.gr.gz"
travel_time_graph_file_path = os.path.join(
network_dir_paths[name], f"USA-road-t.{name}.gr.gz"
)
travel_time_graph_file_paths[name] = travel_time_graph_file_path
# coordinates
coordinates_url = f"http://www.diag.uniroma1.it//challenge9/data/USA-road-d/USA-road-d.{name}.co.gz"
coordinates_file_path = os.path.join(
network_dir_paths[name], f"USA-road-d.{name}.co.gz"
)
coordinates_file_paths[name] = coordinates_file_path
if (not os.path.exists(travel_time_graph_file_path)) & (
not os.path.exists(travel_time_graph_file_path.removesuffix(".gz"))
):
wget.download(travel_time_graph_url, travel_time_graph_file_path)
if (not os.path.exists(coordinates_file_path)) & (
not os.path.exists(coordinates_file_path.removesuffix(".gz"))
):
wget.download(coordinates_url, coordinates_file_path)
Uncompress the network files with gzip
We first create a small function that is looking for a zipped file. If found, the zipped file is uncompressed and removed.
def extract_and_cleanup(file_path_gz):
file_path = file_path_gz.split(".gz")[0]
try:
with gzip.open(file_path_gz, "rb") as f_in:
with open(file_path, "wb") as f_out:
shutil.copyfileobj(f_in, f_out)
os.remove(file_path_gz)
except FileNotFoundError:
pass
return file_path
Now we call the above function extract_and_cleanup for each node and edge file:
for name in names:
# travel time graph
file_path_gz = travel_time_graph_file_paths[name]
file_path = extract_and_cleanup(file_path_gz)
travel_time_graph_file_paths[name] = file_path
# coordinates
file_path_gz = coordinates_file_paths[name]
file_path = extract_and_cleanup(file_path_gz)
coordinates_file_paths[name] = file_path
Create a function to load the edges into a Pandas dataframe
Let’s have a look at one of the edge file:
! head -n 10 {travel_time_graph_file_paths["NY"]}
c 9th DIMACS Implementation Challenge: Shortest Paths
c http://www.dis.uniroma1.it/~challenge9
c TIGER/Line graph USA-road-t.NY
c
p sp 264346 733846
c graph contains 264346 nodes and 733846 arcs
c
a 1 2 2008
a 2 1 2008
a 3 4 395
So we need to skip the header lines, starting either with c or p. Then, on each edge line, we have the letter a, the source node index, the target node index and edge travel time. The edge weight has an int type here and we do not know the time unit. We assume that it corresponds to hundreds of seconds. This also does not matter regarding the comparison of various shortest path implementations.
So once the file is loaded with pandas.read_csv, we perform a few transformation steps:
- set the weight column to
floattype, and convert the weight from hundreds of seconds to seconds - remove parallel edges by keeping a single edge with the min weight
- remove loops, if there is any
- shift the source and target indices by -1 in order to be 0-based
The point of removing parallel arcs, is to get a simple directed graphs, that we can represent with an adjacency matrix in a sparse format. Loops could be described in an adjacency matrix but they would be completely useless regarding shortest paths, the edge weights being non-negative.
def read_travel_time_graph(file_path):
# read the header
with open(file_path) as f:
lines = f.readlines(10_000)
header_size = 0
for line in lines:
header_size += 1
if line.startswith("p"):
# we read the edge count from the header
edge_count = int(line.split(" ")[-1])
elif line.startswith("a"):
header_size -= 1
break
# read the data
df = pd.read_csv(
file_path,
sep=" ",
names=["a", "source", "target", "weight"],
usecols=["source", "target", "weight"],
skiprows=header_size,
)
assert len(df) == edge_count
# data preparation and assertions
assert not df.isna().any().any() # no missing values
df.weight = df.weight.astype(float) # convert to float type
df.weight *= 0.01 # convert to seconds
assert df.weight.min() >= 0.0 # make sure travel times are non-negative
df = (
df.groupby(["source", "target"], sort=False).min().reset_index()
) # remove parallel edges and keep the one with shortest weight
df = df[df["source"] != df["target"]] # remove loops
df[["source", "target"]] -= 1 # switch to 0-based indices
return df
We can try read_travel_time_graph on the NY network file:
file_path = travel_time_graph_file_paths["NY"]
edges_df = read_travel_time_graph(file_path)
edges_df.head(3)
| source | target | weight | |
|---|---|---|---|
| 0 | 0 | 1 | 20.08 |
| 1 | 0 | 11 | 21.05 |
| 2 | 0 | 1362 | 60.70 |
Create a function to load the node coordinates into a Pandas dataframe
The node coordinate files are similar to the edge files:
! head -n 10 {coordinates_file_paths["NY"]}
c 9th DIMACS Implementation Challenge: Shortest Paths
c http://www.dis.uniroma1.it/~challenge9
c TIGER/Line nodes coords for graph USA-road-d.NY
c
p aux sp co 264346
c graph contains 264346 nodes
c
v 1 -73530767 41085396
v 2 -73530538 41086098
v 3 -73519366 41048796
We also need to skip the header lines, starting either with c or p. Then, on each edge line, we have the letter v, the node index, the longitude and latitude. From what I understand, the coordinates are expressed in WGS 84, but as int type, in millionth of degrees. So we divide the int longitude and latitude numbers by a million to obtain the coordinates in degrees.
def read_coords(file_path, epsg=4326):
# read the header
with open(file_path) as f:
lines = f.readlines(10_000)
header_size = 0
for line in lines:
header_size += 1
if line.startswith("p"):
vertex_count = int(line.split(" ")[-1])
elif line.startswith("v"):
header_size -= 1
break
# read the data
df = pd.read_csv(
file_path,
sep=" ",
names=["v", "id", "lng", "lat"],
usecols=["id", "lng", "lat"],
skiprows=header_size,
)
df["id"] -= 1 # 0-based indices
df[["lng", "lat"]] /= 10**6 # convert the coordinates to degrees
if epsg != 4326:
gpd.options.use_pygeos = True
# load the vertices into a geodataframe
gdf = gpd.GeoDataFrame(
df, geometry=gpd.points_from_xy(df.lng, df.lat), crs="EPSG:4326" # WGS 84
)
gdf.drop(["lng", "lat"], axis=1, inplace=True)
gdf.set_index("id", inplace=True)
nodes_gs = gdf.geometry
nodes_gs = nodes_gs.to_crs(epsg=epsg)
nodes_gdf = nodes_gs.to_frame("geometry")
nodes_gdf["x"] = nodes_gdf.geometry.x
nodes_gdf["y"] = nodes_gdf.geometry.y
nodes_df = nodes_gdf[["x", "y"]]
else:
nodes_df = df.rename(columns={"lng": "x", "lat": "y"})
nodes_df.set_index("id", inplace=True)
assert len(nodes_df) == vertex_count
return nodes_df
Let’s run read_coords on the NY network file:
file_path = coordinates_file_paths["NY"]
nodes_df = read_coords(file_path)
nodes_df.head(3)
| x | y | |
|---|---|---|
| id | ||
| 0 | -73.530767 | 41.085396 |
| 1 | -73.530538 | 41.086098 |
| 2 | -73.519366 | 41.048796 |
We added an argument epsg with a target CRS. This is, for the case where we would like to use a different CRS than EPSG:4326. GeoPandas is used to transform the data in that case.
nodes_df = read_coords(file_path, epsg=3857)
nodes_df.head(3)
| x | y | |
|---|---|---|
| id | ||
| 0 | -8.185408e+06 | 5.024946e+06 |
| 1 | -8.185382e+06 | 5.025049e+06 |
| 2 | -8.184138e+06 | 5.019542e+06 |
Save the networks into parquet files
Now we call both functions, read_travel_time_graph and read_coords, for all the networks and write the corresponding dataframes as parquet files.
parquet_tt_file_paths = {}
for name in names:
file_path = travel_time_graph_file_paths[name]
parquet_tt_file_path = file_path + ".parquet"
parquet_tt_file_paths[name] = parquet_tt_file_path
if not os.path.exists(parquet_tt_file_path):
edges_df = read_travel_time_graph(file_path)
edges_df.to_parquet(parquet_tt_file_path)
parquet_coord_file_paths = {}
for name in names:
file_path = coordinates_file_paths[name]
parquet_coord_file_path = file_path + ".parquet"
if not os.path.exists(parquet_coord_file_path):
nodes_df = read_coords(file_path)
nodes_df.to_parquet(parquet_coord_file_path)
parquet_coord_file_paths[name] = parquet_coord_file_path
We now have all the parquet files ready for use on the disk!
!tree -P '*.parquet' {data_dir_path}
/home/francois/Data/Disk_1/DIMACS_road_networks
├── BAY
│ ├── USA-road-d.BAY.co.parquet
│ └── USA-road-t.BAY.gr.parquet
├── CAL
│ ├── USA-road-d.CAL.co.parquet
│ └── USA-road-t.CAL.gr.parquet
├── COL
│ ├── USA-road-d.COL.co.parquet
│ └── USA-road-t.COL.gr.parquet
├── CTR
│ ├── USA-road-d.CTR.co.parquet
│ └── USA-road-t.CTR.gr.parquet
├── E
│ ├── USA-road-d.E.co.parquet
│ └── USA-road-t.E.gr.parquet
├── FLA
│ ├── USA-road-d.FLA.co.parquet
│ └── USA-road-t.FLA.gr.parquet
├── LKS
│ ├── USA-road-d.LKS.co.parquet
│ └── USA-road-t.LKS.gr.parquet
├── NE
│ ├── USA-road-d.NE.co.parquet
│ └── USA-road-t.NE.gr.parquet
├── NW
│ ├── USA-road-d.NW.co.parquet
│ └── USA-road-t.NW.gr.parquet
├── NY
│ ├── USA-road-d.NY.co.parquet
│ └── USA-road-t.NY.gr.parquet
├── USA
│ ├── USA-road-d.USA.co.parquet
│ └── USA-road-t.USA.gr.parquet
└── W
├── USA-road-d.W.co.parquet
└── USA-road-t.W.gr.parquet
12 directories, 24 files
Query the parquet files with DuckDB
Although we could have done it earlier when we had the dataframes in our hands, we are now going to perform some basic analysis of the networks. The motivation is to clearly separate the different steps.
We want to count the number of edges and vertices in each network, from the parquet files, without loading all the data into memory, and rather in an efficient way. We are going to compute these network features using some SQL, with DuckDB.
%%time
network_info = []
for name in names:
parquet_tt_file_path = parquet_tt_file_paths[name]
query = f"""SELECT COUNT(*), MAX(source), MAX(target) FROM parquet_scan('{parquet_tt_file_path}')"""
res = duckdb.query(query).fetchall()[0]
edge_count = res[0]
vertex_count = np.max(res[1:3]) + 1
query = f"""
WITH edges AS (SELECT
source,
target
FROM
parquet_scan('{parquet_tt_file_path}'))
SELECT
COUNT(DISTINCT node)
FROM
( SELECT
source AS node
FROM
edges
UNION ALL
SELECT
target AS node
FROM
edges
)"""
used_vertices = duckdb.query(query).fetchone()[0]
mean_degree = edge_count / used_vertices
network_info.append(
{
"name": name,
"vertex_count": vertex_count,
"used_vertices": used_vertices,
"edge_count": edge_count,
"mean_degree": mean_degree,
}
)
CPU times: user 1min 16s, sys: 3.96 s, total: 1min 20s
Wall time: 43.6 s
network_info_df = pd.DataFrame(network_info).set_index("name")
network_info_df = network_info_df.sort_values(by=["edge_count"])
pd.set_option("display.precision", 2)
network_info_df
| vertex_count | used_vertices | edge_count | mean_degree | |
|---|---|---|---|---|
| name | ||||
| NY | 264346 | 264346 | 730100 | 2.76 |
| BAY | 321270 | 321270 | 794830 | 2.47 |
| COL | 435666 | 435666 | 1042400 | 2.39 |
| FLA | 1070376 | 1070376 | 2687902 | 2.51 |
| NW | 1207945 | 1207945 | 2820774 | 2.34 |
| NE | 1524453 | 1524453 | 3868020 | 2.54 |
| CAL | 1890815 | 1890815 | 4630444 | 2.45 |
| LKS | 2758119 | 2758119 | 6794808 | 2.46 |
| E | 3598623 | 3598623 | 8708058 | 2.42 |
| W | 6262104 | 6262104 | 15119284 | 2.41 |
| CTR | 14081816 | 14081816 | 33866826 | 2.41 |
| USA | 23947347 | 23947347 | 57708624 | 2.41 |
We can observe that all the vertices are actually used in the graph. The mean degree does not vary too much, although it it a little larger in the NY area, which is densely populated.
Plot the networks with Datashader
Finally, we are going to plot some of these networks using Datashader.
But before that, we also want to print a rough approximation of the network width and height. Because we have the coordinates expressed in WGS84, let’s write a small function to compute an approximate distance in meters between two points, given their lat/lon coordinates. This is a straight implementation of Haversine formula.
def haversine_distance(lon_1, lat_1, lon_2, lat_2):
"""Calculate the distance between two points using their latitude and longitude."""
phi_1, phi_2 = np.radians(lat_1), np.radians(lat_2)
delta_phi = np.radians(lat_2 - lat_1)
delta_lambda = np.radians(lon_2 - lon_1)
a = (
np.sin(0.5 * delta_phi) ** 2
+ np.cos(phi_1) * np.cos(phi_2) * np.sin(0.5 * delta_lambda) ** 2
)
c = 2.0 * np.arctan2(np.sqrt(a), np.sqrt(1 - a))
R = 6.371e6 # approximate earth radius
d_m = R * c
return d_m
Now the following load_and_plot function is actually loading the vertex and edge dataframes from the respective parquet files. Then both are used in Datashader’s connect_edges function. The Datashader part is strongly inspired from its documentation about networks.
def load_and_plot(
name,
parquet_coord_file_paths,
parquet_tt_file_paths,
network_info_df,
plot_width=1200,
):
# load the network
parquet_coord_file_path = parquet_coord_file_paths[name]
nodes_df = pd.read_parquet(parquet_coord_file_path)
parquet_tt_file_path = parquet_tt_file_paths[name]
edges_df = pd.read_parquet(parquet_tt_file_path, columns=["source", "target"])
edges_df = edges_df.astype(np.uintc)
# compute the network width and height
xr = nodes_df.x.min(), nodes_df.x.max()
yr = nodes_df.y.min(), nodes_df.y.max()
width_km = 0.001 * haversine_distance(xr[0], yr[0], xr[1], yr[0])
height_km = 0.001 * haversine_distance(xr[0], yr[0], xr[0], yr[1])
print(f"Network : {name}")
print(
f"width : {int(round(width_km)):6d} km, height : {int(round(height_km)):6d} km"
)
vertex_count = network_info_df.loc[name, "vertex_count"]
edge_count = network_info_df.loc[name, "edge_count"]
print(f"vertex count : {vertex_count}, edge count : {edge_count}")
# plot the network
edges_ds = connect_edges(nodes_df, edges_df)
plot_height = int(plot_width * (yr[1] - yr[0]) / (xr[1] - xr[0]))
cvsopts = dict(plot_height=plot_height, plot_width=plot_width)
canvas = ds.Canvas(x_range=xr, y_range=yr, **cvsopts)
ep = tf.spread(
tf.shade(canvas.line(edges_ds, "x", "y", agg=ds.count()), cmap=["#F03811"]),
px=0,
)
return ep
load_and_plot("NY", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : NY
width : 85 km, height : 111 km
vertex count : 264346, edge count : 730100

load_and_plot("BAY", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : BAY
width : 178 km, height : 222 km
vertex count : 321270, edge count : 794830

load_and_plot("COL", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : COL
width : 621 km, height : 445 km
vertex count : 435666, edge count : 1042400

load_and_plot("FLA", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : FLA
width : 753 km, height : 680 km
vertex count : 1070376, edge count : 2687902
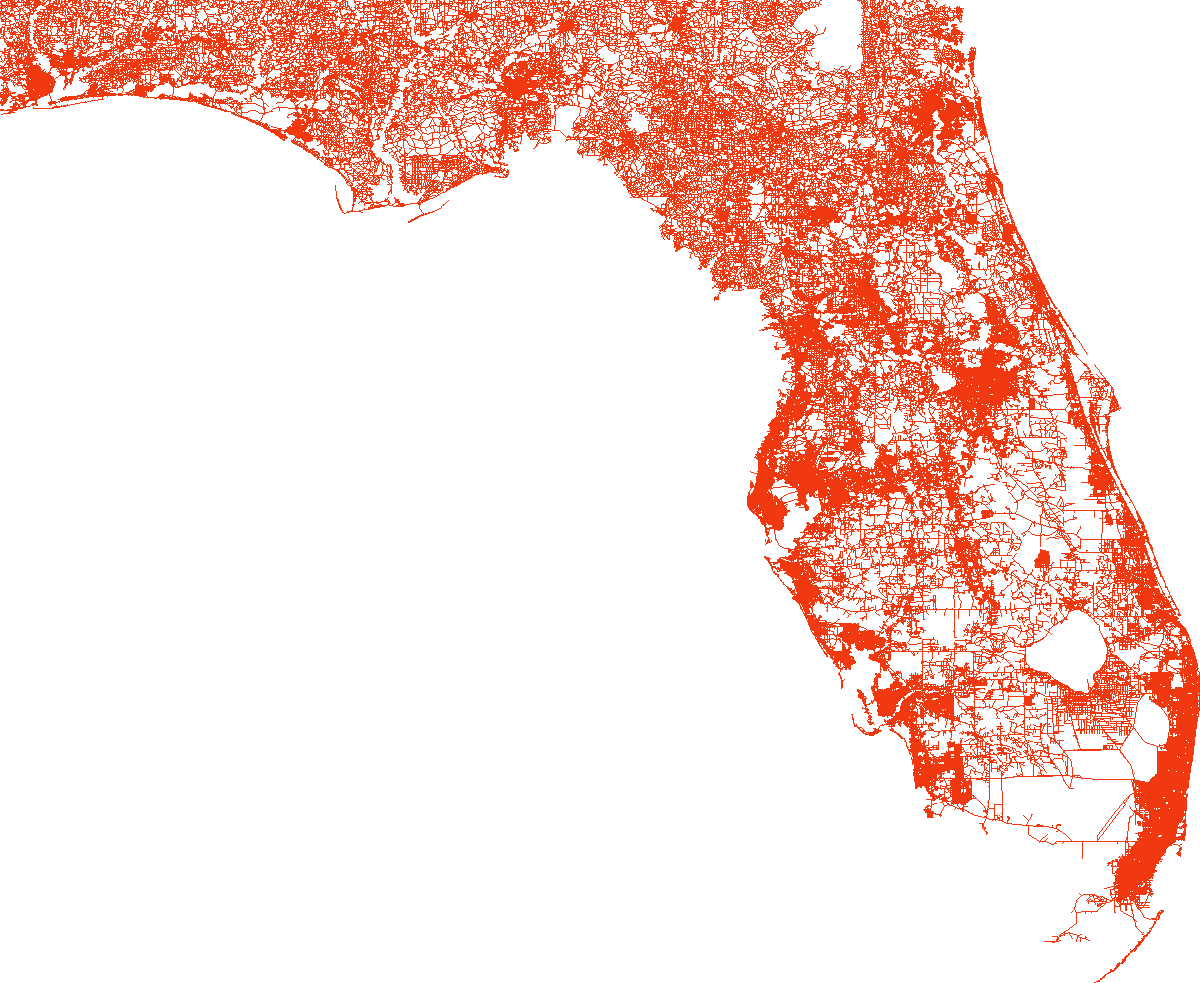
load_and_plot("NW", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : NW
width : 720 km, height : 779 km
vertex count : 1207945, edge count : 2820774

load_and_plot("NE", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : NE
width : 520 km, height : 389 km
vertex count : 1524453, edge count : 3868020

load_and_plot("CAL", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : CAL
width : 976 km, height : 1056 km
vertex count : 1890815, edge count : 4630444

load_and_plot("LKS", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : LKS
width : 1591 km, height : 827 km
vertex count : 2758119, edge count : 6794808
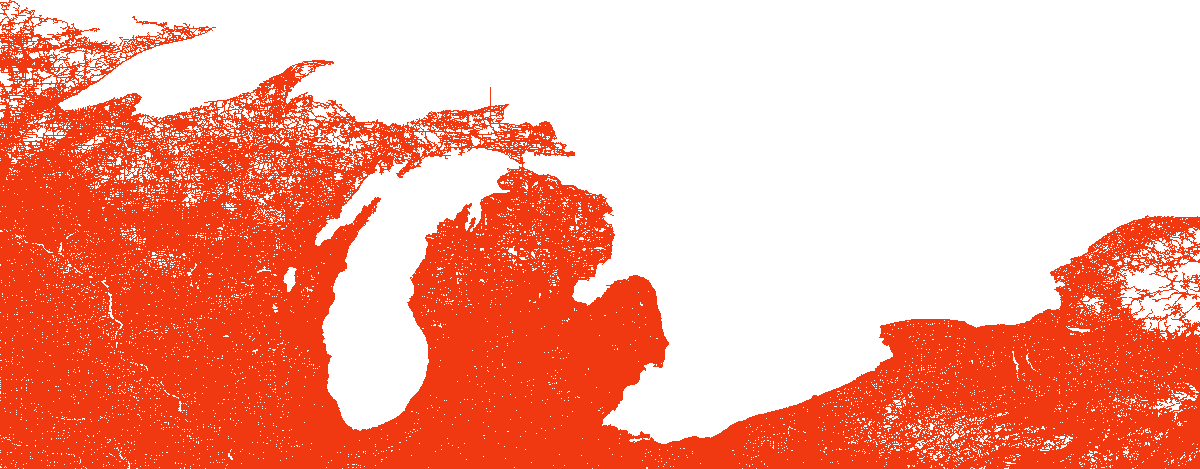
load_and_plot("E", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : E
width : 1116 km, height : 1543 km
vertex count : 3598623, edge count : 8708058
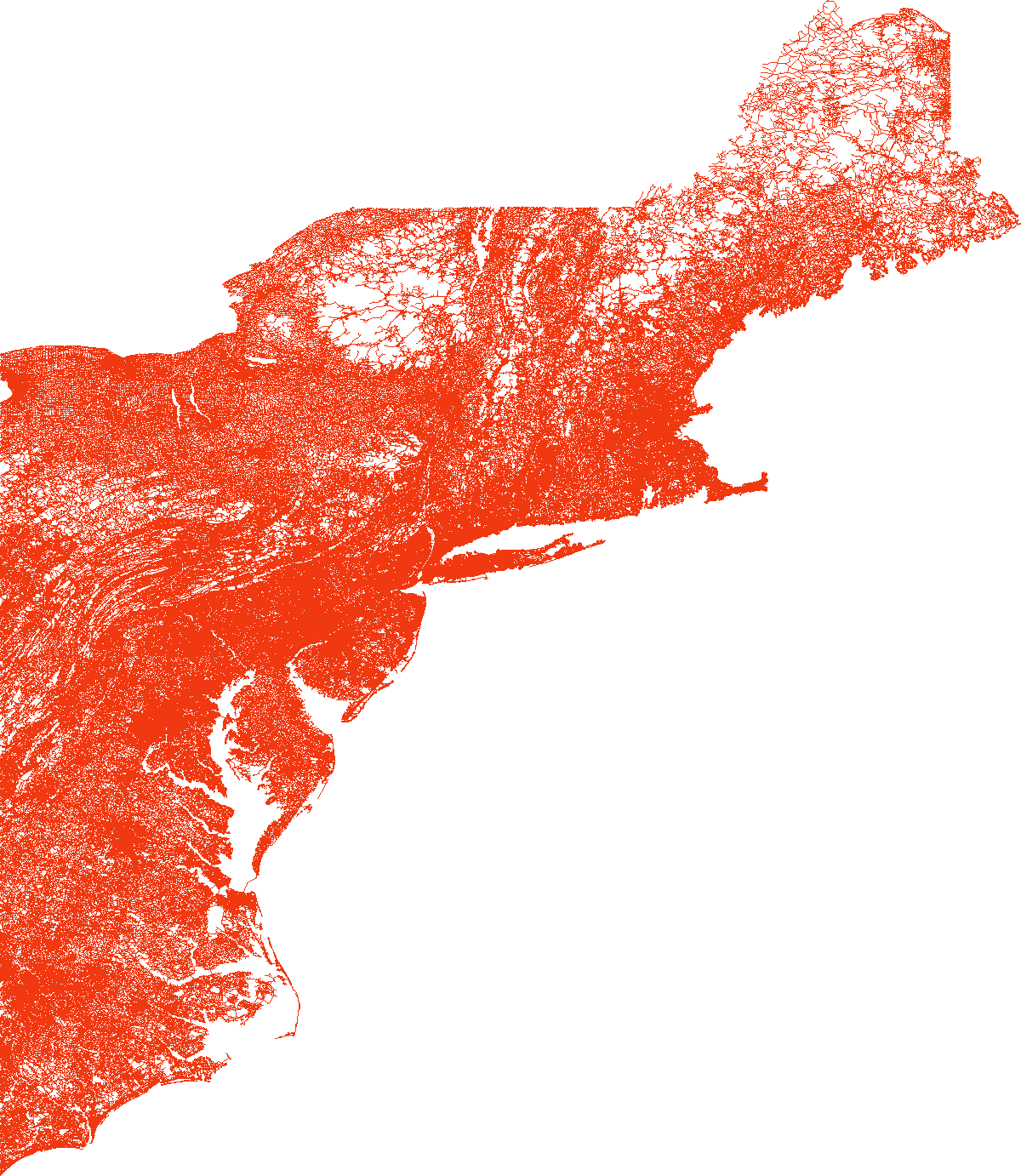
load_and_plot("W", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : W
width : 2422 km, height : 2331 km
vertex count : 6262104, edge count : 15119284
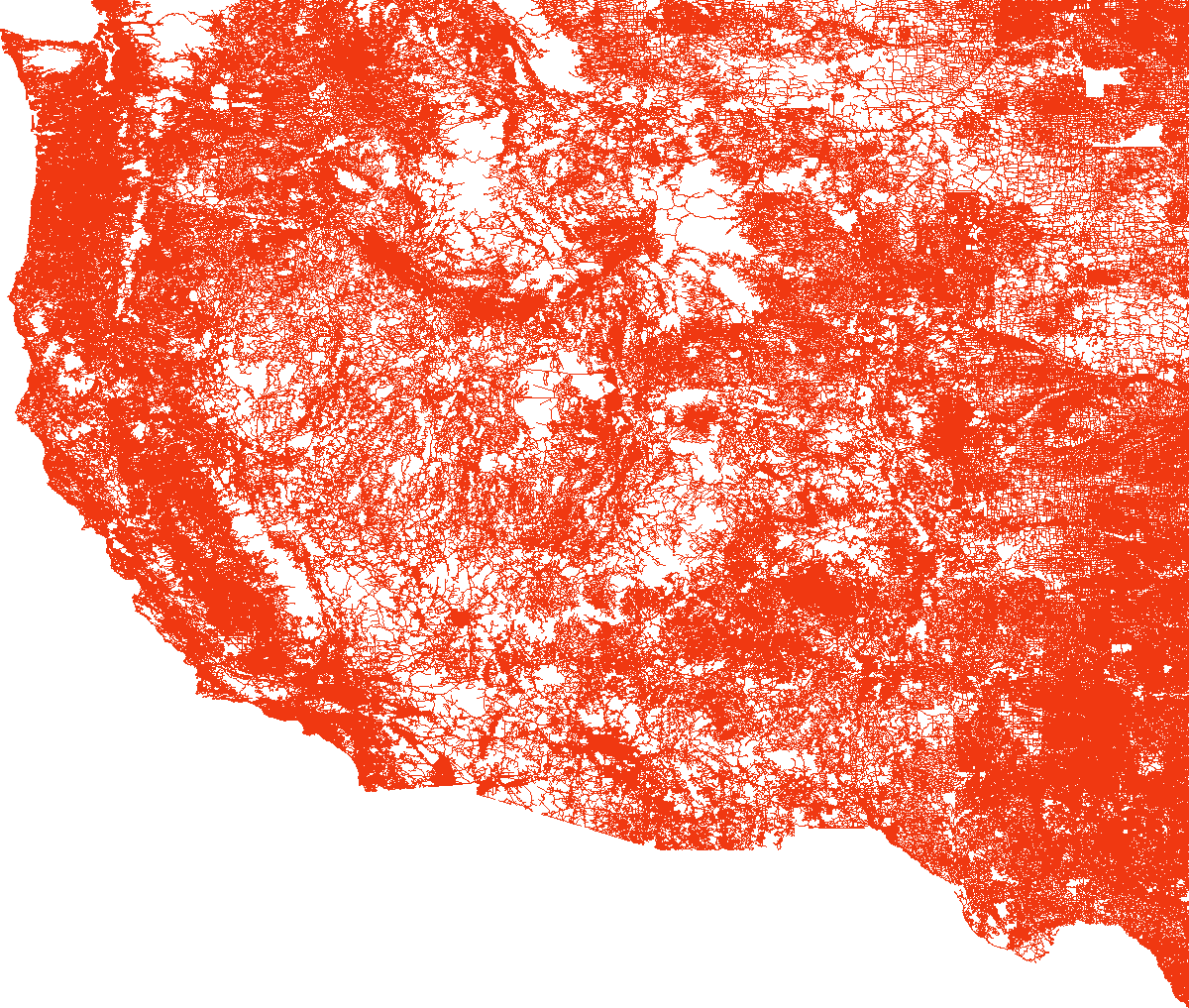
load_and_plot("CTR", parquet_coord_file_paths, parquet_tt_file_paths, network_info_df)
Network : CTR
width : 2114 km, height : 2669 km
vertex count : 14081816, edge count : 33866826
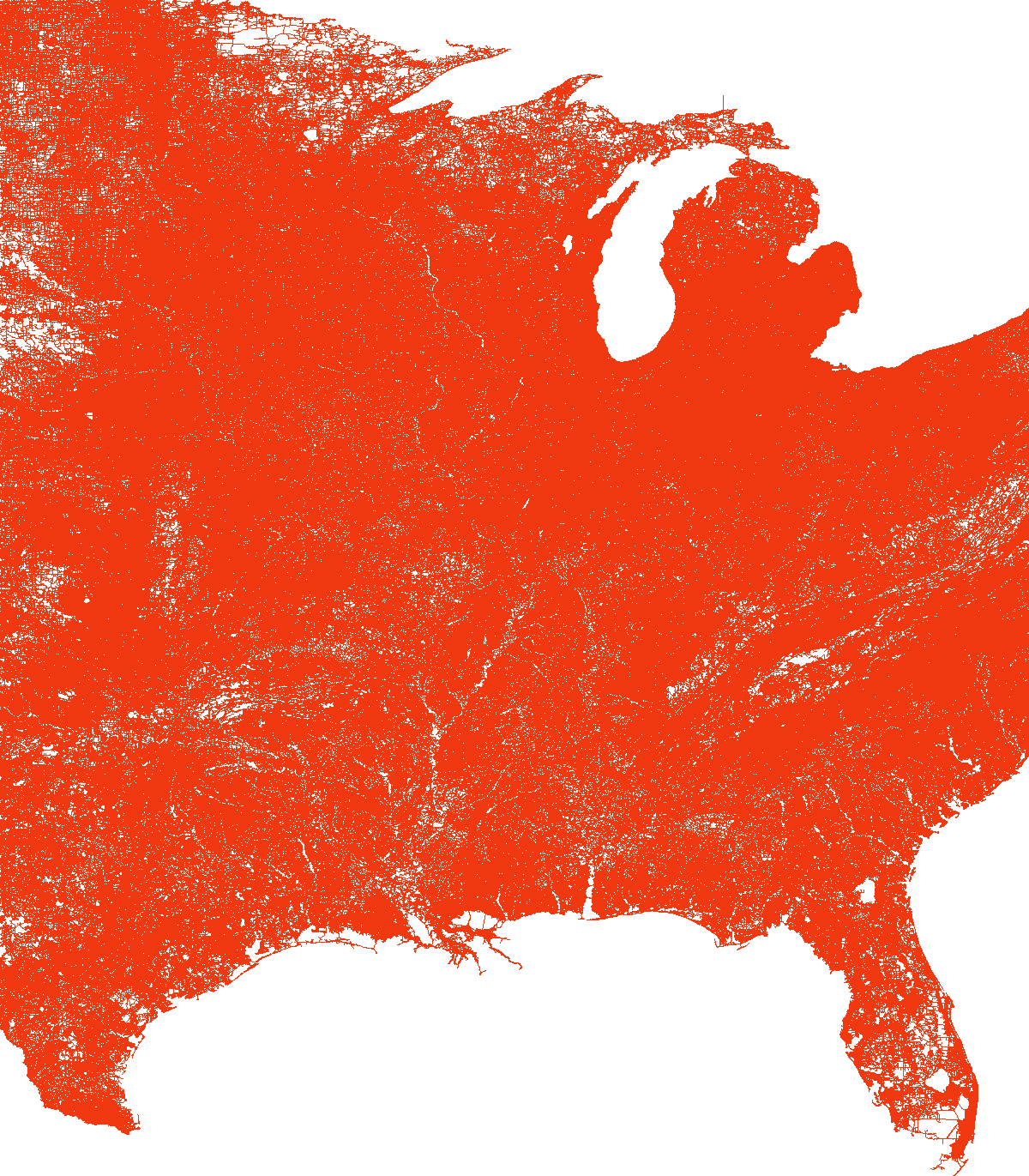
We note that it is hard to distinguish anything in the last plot because of the network large size, with a fixed size plot and a fixed edge width. Also I couldn’t plot the largest one, USA, for some memory reasons.
The networks are now ready to be use by some Shortest Path algorithms, which will be the subject of some future posts.