Visualizing the Ulam Spiral with Python

The Ulam spiral arranges integers in a spiral and highlights prime numbers, revealing some diagonal alignment patterns. This post shows how to generate and visualize the Ulam spiral in Python, with a simple prime-checking implementation using Cython.

As described in the Wikipedia article on the Ulam spiral:

According to Gardner, Ulam discovered the spiral in 1963 while doodling during the presentation of “a long and very boring paper” at a scientific meeting. These hand calculations amounted to “a few hundred points”. Shortly afterwards, Ulam, with collaborators Myron Stein and Mark Wells, used MANIAC II at Los Alamos Scientific Laboratory to extend the calculation to about 100,000 points. The group also computed the density of primes among numbers up to 10,000,000 along some of the prime-rich lines as well as along some of the prime-poor lines.

Originally uploaded by Deer*lake (Transferred by Deer*lake), Public domain, via Wikimedia Commons

Imports

We use a Python 3.13.0 environment packaged by conda-forge on Linux.

import cython
import matplotlib.pyplot as plt
import numpy as np

%load_ext cython

FS = (12, 12)  # figure size

Package versions:

cython     :  3.0.11
matplotlib :  3.9.2
numpy      :  2.1.3

Prime Number Check: is_prime function

To check for prime numbers, we use a method described in the Wikipedia article on primality testing:

Observe that all primes greater than 3 are of the form $6k+i$ for a nonnegative integer $k$ and $i\in {1,5}$. Indeed, every integer is of the form $6k+i$ for a positive integer $k$ and $i\in {0,1,2,3,4,5}$. Since 2 divides $6k,6k+2$, and $6k+4$, and 3 divides $6k$ and $6k+3$, the only possible remainders mod 6 for a prime greater than 3 are 1 and 5. So, a more efficient primality test for $n$ is to test whether $n$ is divisible by 2 or 3, then to check through all numbers of the form $6k+1$ and $6k+5$ which are $\leq {\sqrt {n}}$. This is almost three times as fast as testing all numbers up to $\sqrt {n}$.

The implementation below uses this approach to determine primality:

def is_prime(n):

    if n <= 1:
        return 0
    elif n <= 3:
        return 1
    else:

        if np.mod(n, 2) == 0:
            return 0
        if np.mod(n, 3) == 0:
            return 0

        ub = int(np.floor(np.sqrt(n)))
        
        k = 0
        d = 5
        while d <= ub:

            if np.mod(n, d) == 0:
                return 0
            
            k += 1
            d = 6 * k + 5
        
        k = 1
        d = 7
        while d <= ub:

            if np.mod(n, d) == 0:
                return 0

            k += 1
            d = 6 * k + 1

    return 1

The function is tested on integers from 0 to 99, producing the following primes:

for n in range(100):
    if is_prime(n):
        print(n, end=" ")

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

Optimizing with Cython

The function is_prime_cython implements the same logic as our Python version but is optimized with Cython’s cdef declarations for fixed-size integers.

The generate_ulam_spiral function creates a 2D array representing the Ulam spiral. The grid starts at the center and spirals outward, marking cells as prime or non-prime using the is_prime_cython function. The directions sequence defines the movement pattern for generating the Ulam spiral, specifying steps in the order: up, left, down, and right, with each direction represented as a pair of (dx, dy) offsets. Each step size is used twice, once for each direction pair (“up” and “left”, or “down” and “right”) before increasing the step size, maintaining the spiral’s consistent growth pattern.

Note that the grid size must be odd to ensure that there is a well-defined center point from which the spiral can start expanding symmetrically outward.

%%cython --compile-args=-Ofast

# cython: language_level=3, boundscheck=False, wraparound=False, embedsignature=False, initializedcheck=False
# distutils: define_macros=NPY_NO_DEPRECATED_API=NPY_1_7_API_VERSION

import numpy as np

cimport numpy as cnp


cdef cnp.uint8_t is_prime_cython(size_t n):
    """Check if a number is prime."""
    cdef size_t k, ub, d

    if n <= 1:
        return 0
    elif n <= 3:
        return 1
    else:

        if np.mod(n, 2) == 0:
            return 0
        if np.mod(n, 3) == 0:
            return 0

        ub = <size_t>(np.floor(np.sqrt(n)))
        
        k = 0
        d = 5
        while d <= ub:

            if np.mod(n, d) == 0:
                return 0
            
            k += 1
            d = 6 * k + 5
        
        k = 1
        d = 7
        while d <= ub:

            if np.mod(n, d) == 0:
                return 0

            k += 1
            d = 6 * k + 1

    return 1


cpdef generate_ulam_spiral(int size):
    """Function to generate the Ulam spiral as a 2D array."""
    cdef: 
        size_t num = 1  # start numbering from 1
        size_t step_size = 1  # number of steps to take in the current direction
        int x = size // 2, y = size // 2  # start at the center

    if np.mod(size, 2) == 0:
        raise ValueError("Grid size must be an odd number.")
    
    grid = np.zeros((size, size), dtype=np.byte)

    # Define the directions: up, left, down, right
    directions = [(0, 1), (-1, 0), (0, -1), (1, 0)]
    direction_index = 0  # Start moving to the top

    while num <= <size_t>(size * size):
        for _ in range(2):  # repeat for two turns for each step size
            for _ in range(step_size):  # move in the current direction
                if 0 <= x < size and 0 <= y < size:
                    if is_prime_cython(num):
                        grid[size - y - 1, x] = 1  # mark as prime
                x += directions[direction_index][0]
                y += directions[direction_index][1]
                num += 1
                if num > <size_t>(size * size):  # stop if we've filled the grid
                    break
            direction_index = np.mod(direction_index + 1, 4)  # change direction
        step_size += 1  # increase the step size after every two turns

    return grid

Note that in order to properly display the Ulam spiral, the 2D grid is flipped upside down in the following code line: grid[size - y - 1, x] = 1.

Computing the Grid Size for the Ulam Spiral

The compute_grid_size function calculates the minimal odd-sized square grid required to represent the first n integers in the Ulam spiral. It ensures that the grid size is large enough to accommodate the given range of numbers and is always odd, as required for the spiral’s center to align properly.

def compute_grid_size(n=100):
    """
    Calculate the minimal odd size of a square grid needed to store
    flags for the first `n` integers.
    """
    size = int(np.ceil(np.sqrt(n)))
    if np.mod(size, 2) == 0:
        size += 1
    return size

The plot_ulam_spiral function generates and visualizes the Ulam spiral. It takes either a specified grid size or the number of integers n to determine the minimal grid size, and then uses the generate_ulam_spiral function to create and display the spiral.

def plot_ulam_spiral(size=None, n=None, figsize=(8, 8)):
    """
    Plot the Ulam spiral, a visual representation of prime numbers arranged
    in a spiral pattern.
    """
    if (size is None) and (n is not None):
        size = compute_grid_size(n)
    elif (size is None) and (n is None):
        raise ValueError("Both size and n are missing.")
    elif (size is not None) and (n is not None):
        raise ValueError("Both size and n are given.")
    spiral = generate_ulam_spiral(size)
    plt.figure(figsize=figsize)
    plt.imshow(spiral, cmap="binary", interpolation="nearest")
    plt.axis("off")

Visualizing the Ulam Spiral for Various Values of n

plot_ulam_spiral(n=10, figsize=FS)

plot_ulam_spiral(n=100, figsize=FS)

plot_ulam_spiral(n=1_000, figsize=FS)

plot_ulam_spiral(n=10_000, figsize=FS)

plot_ulam_spiral(n=100_000, figsize=FS)

plot_ulam_spiral(n=1_000_000, figsize=FS)

Prime Numbers in Diagonal Lines of the Ulam Spiral

We can observe that prime numbers tend to collect along diagonal lines. According to the Ulam spiral’s wikipedia page:

Diagonal, horizontal, and vertical lines in the number spiral correspond to polynomials of the form $f(n)=4n^2+bn+c$ where $b$ and $c$ are integer constants. When $b$ is even, the lines are diagonal, and either all numbers are odd, or all are even, depending on the value of $c$. It is therefore no surprise that all primes other than 2 lie in alternate diagonals of the Ulam spiral. Some polynomials, such as $4n^{2}+8n+3$, while producing only odd values, factorize over the integers $(4n^{2}+8n+3)=(2n+1)(2n+3)$ and are therefore never prime except possibly when one of the factors equals 1. Such examples correspond to diagonals that are devoid of primes or nearly so.

Let’s visualize some of the prime-rich quadratic polynomials. The following code defines two functions: is_quadratic, which checks if a number satisfies a given quadratic polynomial equation, and plot_quadratic_lines, which generates and plots an Ulam spiral, marking prime numbers in grey and overlaying quadratic polynomial points as black dots on the spiral.

def is_quadratic(num, a=4, b=8, c=3, eps=1.e-10):
    coeff = [a, b, c - num]
    n_1, _ = np.roots(coeff)
    if np.isreal(n_1):
        if (np.abs(n_1-np.round(n_1)) < eps):
            return 1
    return 0


def plot_quadratic_lines(size=101, a=4, b=8, c=3, figsize=(8,8)):
    """Plot the Ulam spiral with quadratic polynomial points marked as dots."""

    spiral = generate_ulam_spiral(size)
    grid = np.zeros((size, size), dtype=bool)

    num = 1  # start numbering from 1
    step_size = 1  # number of steps to take in the current direction
    x = size // 2
    y = size // 2  # start at the center

    directions = [(0, 1), (-1, 0), (0, -1), (1, 0)]
    direction_index = 0
    quadratic_points = []  # to store coordinates of quadratic points

    # generate the grid and mark primes and quadratic points
    while num <= size * size:
        for _ in range(2):  # repeat for two turns for each step size
            for _ in range(step_size):  # move in the current direction
                if 0 <= x < size and 0 <= y < size:
                    if is_quadratic(num, a=a, b=b, c=c):
                        quadratic_points.append((x, size - y - 1))  # store the coordinates of quadratic points
                    if is_prime(num):  # check if number is prime
                        grid[size - y - 1, x] = 1  # mark primes with 1
                x += directions[direction_index][0]
                y += directions[direction_index][1]
                num += 1
                if num > size * size:  # stop if we've filled the grid
                    break
            direction_index = np.mod(direction_index + 1, 4)  # change direction
        step_size += 1  # increase the step size after every two turns

    n = 1
    
    
    # plot the spiral using binary colormap
    plt.figure(figsize=figsize)
    plt.imshow(grid, cmap="binary", interpolation="nearest", alpha=0.2)
    plt.axis("off")

    # overlay quadratic polynomial points as crosses
    for point in quadratic_points:
        plt.scatter(point[0], point[1], color='k', s=20, marker='.')  

    plt.show()

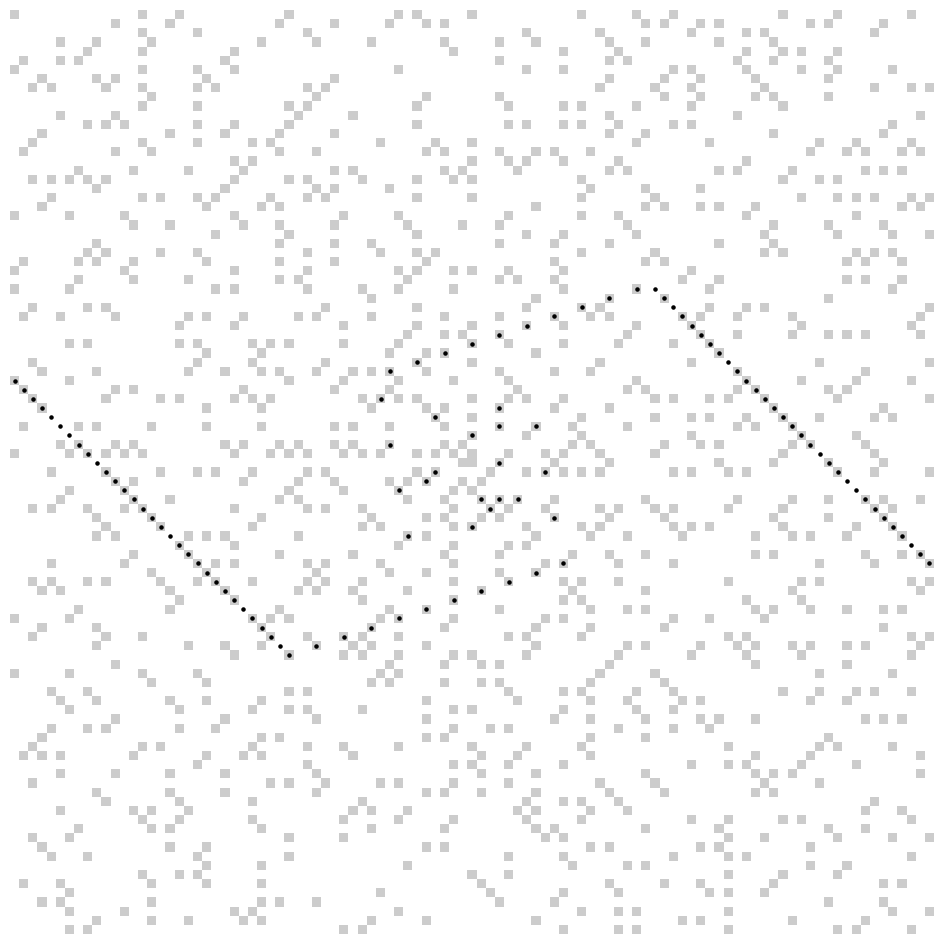
Let’s visualize the diagonal that is devoid of primes or nearly so, corresponding to $f(n)=4n^2+8n+3$:

plot_quadratic_lines(size=101, a=4, b=8, c=3, figsize=FS)

We have $f(0)=3$, which is the only prime belonging to the dotted line in the above figure. Let’s check Euler’s prime-generating polynomial $f(n)=n^2−n+41$:

Lastly, there is also Legendre’s polynomial $f(n)=n^2+n+17$:

See this Wolfram’s web page for a list of prime-generating polynomials.