Merge Sort with Cython and Numba
In this post, we present an implementation of the classic merge sort algorithm in Python on NumPy arrays, and make it run reasonably “fast” using Cython and Numba. We are going to compare the run time with the numpy.sort(kind='mergesort') implementation (in C). We already applied both tools to insertion sort in a previous post. Let’s start by briefly describing the merge sort algorithm.
Merge sort
Here is the main idea of merge sort (from wikipedia):
Conceptually, a merge sort works as follows:
- Divide the unsorted list into $n$ sublists, each containing one element (a list of one element is considered sorted).
- Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.
The performance of merge sort is $O(n\log{}n)$ independently of the input order: worst case and average case have the same complexities. We refer to any classic book about algorithms to get more theoretical and practical insights about this algorithm.
Top-down implementation
Here we are going to implement a top-down version of the algorithm for arrays: it is a divide-and-conquer recursive approach that we can describe with the following simplified code:
def mergesort(A, l, r):
if l < r:
mid = l + int((r - l) / 2)
mergessort(A, l, mid) # sort the left sub-array recursively
mergesort(A, m + 1, r) # sort the right sub-array recursively
merge(A, l, mid, r)
mergesort(A, 0, len(A) - 1)
The merge part consists in sorting two sorted contiguous chunks of arrays.
Implementation optimizations
An additional storage is used during the merge step, which size is of the order of $n$. This also implies copying back the merged list from the auxiliary array(s) back to $A$, which has a cost. It is possible to implement the algorithm without copying, which is what we chose to do in the following. As explained by Robert Sedgewick in [1]:
To do so, we arrange the recursive calls such that the computation switches the roles of the input array and the auxiliary array at each level.
Here are the optimizations performed in the following implementation:
- Eliminate the copy to the auxiliary array (reducing the cost of copying).
- Use an in-place sorting algorithm (
insertion sort) for small subarrays (length smaller than a constantSMALL_MERGESORT=40). This may be referred to as tiled merge sort. - Stop if already sorted (test if the array is already in order before merging :
A[mid] <= A[mid + 1]).
[1] Robert Sedgewick. Algorithms in C: Parts 1-4, Fundamentals, Data Structures, Sorting, and Searching (3rd. ed.). Addison-Wesley Longman Publishing Co., Inc., USA. 1997.
Imports
import numpy as np
import matplotlib.pyplot as plt
import perfplot
from numba import jit
%load_ext Cython
np.random.seed(124) # Just a habit
Here are the package versions:
Python : 3.8.6
numpy : 1.19.4
perfplot : 0.8.1
cython : 0.29.21
numba : 0.52.0
matplotlib: 3.3.3
Test array
We create a small NumPy int64 array in order to test the different implementations.
N = 1000
A = np.random.randint(low=0, high=10 * N, size=N, dtype=np.int64)
A[:5]
array([4558, 4764, 8327, 9154, 681])
Cython implementation
The Cython implementation can only sort NumPy int64 arrays. The functions should be duplicated and specialized to each supported type (e.g. float64).
%%cython --compile-args=-Ofast
import cython
import numpy as np
cimport numpy as cnp
ctypedef cnp.int64_t stype
cdef Py_ssize_t SMALL_MERGESORT_CYTHON = 40
@cython.boundscheck(False)
@cython.wraparound(False)
@cython.initializedcheck(False)
@cython.binding(False)
cdef void merge_cython(
stype[:] A,
stype[:] Aux,
Py_ssize_t lo,
Py_ssize_t mid,
Py_ssize_t hi) nogil:
cdef:
Py_ssize_t i, j, k
i = lo
j = mid + 1
for k in range(lo, hi + 1):
if i > mid:
Aux[k] = A[j]
j += 1
elif j > hi:
Aux[k] = A[i]
i += 1
elif A[j] < A[i]:
Aux[k] = A[j]
j += 1
else:
Aux[k] = A[i]
i += 1
@cython.boundscheck(False)
@cython.wraparound(False)
@cython.initializedcheck(False)
@cython.binding(False)
cdef void insertion_sort_cython(
stype[:] A,
Py_ssize_t lo,
Py_ssize_t hi) nogil:
cdef:
Py_ssize_t i, j
stype key
for i in range(lo + 1, hi + 1):
key = A[i]
j = i - 1
while (j >= lo) & (A[j] > key):
A[j + 1] = A[j]
j -= 1
A[j + 1] = key
@cython.boundscheck(False)
@cython.wraparound(False)
@cython.initializedcheck(False)
@cython.binding(False)
cdef void merge_sort_cython(
stype[:] A,
stype[:] Aux,
Py_ssize_t lo,
Py_ssize_t hi) nogil:
cdef Py_ssize_t i, mid
if (hi - lo > SMALL_MERGESORT_CYTHON):
mid = lo + ((hi - lo) >> 1)
merge_sort_cython(Aux, A, lo, mid)
merge_sort_cython(Aux, A, mid + 1, hi)
if A[mid] > A[mid + 1]:
merge_cython(A, Aux, lo, mid, hi)
else:
for i in range(lo, hi + 1):
Aux[i] = A[i]
else:
insertion_sort_cython(Aux, lo, hi)
cpdef merge_sort_main_cython(A):
B = np.copy(A)
Aux = np.copy(A)
merge_sort_cython(Aux, B, 0, len(B) - 1)
return B
B = merge_sort_main_cython(A)
np.testing.assert_array_equal(B, np.sort(A))
Numba implementation
The Numba implementation can sort any NumPy numeric type.
Also, we are using the Numba nopython mode. From Numba’s documentation:
Numba has two compilation modes: nopython mode and object mode. The former produces much faster code, but has limitations that can force Numba to fall back to the latter. To prevent Numba from falling back, and instead raise an error, pass
nopython=True.
SMALL_MERGESORT_NUMBA = 40
@jit(nopython=True)
def merge_numba(A, Aux, lo, mid, hi):
i = lo
j = mid + 1
for k in range(lo, hi + 1):
if i > mid:
Aux[k] = A[j]
j += 1
elif j > hi:
Aux[k] = A[i]
i += 1
elif A[j] < A[i]:
Aux[k] = A[j]
j += 1
else:
Aux[k] = A[i]
i += 1
@jit(nopython=True)
def insertion_sort_numba(A, lo, hi):
for i in range(lo + 1, hi + 1):
key = A[i]
j = i - 1
while (j >= lo) & (A[j] > key):
A[j + 1] = A[j]
j -= 1
A[j + 1] = key
@jit(nopython=True)
def merge_sort_numba(A, Aux, lo, hi):
if hi - lo > SMALL_MERGESORT_NUMBA:
mid = lo + ((hi - lo) >> 1)
merge_sort_numba(Aux, A, lo, mid)
merge_sort_numba(Aux, A, mid + 1, hi)
if A[mid] > A[mid + 1]:
merge_numba(A, Aux, lo, mid, hi)
else:
for i in range(lo, hi + 1):
Aux[i] = A[i]
else:
insertion_sort_numba(Aux, lo, hi)
@jit(nopython=True)
def merge_sort_main_numba(A):
B = np.copy(A)
Aux = np.copy(A)
merge_sort_numba(Aux, B, 0, len(B) - 1)
return B
B = merge_sort_main_numba(A)
np.testing.assert_array_equal(B, np.sort(A))
Timings
out = perfplot.bench(
setup=lambda n: np.random.randint(low=0, high=10 * n, size=n, dtype=np.int64),
kernels=[
lambda A: merge_sort_main_cython(A),
lambda A: merge_sort_main_numba(A),
lambda A: np.sort(A, kind="mergesort"),
],
labels=["Cython", "Numba", "NumPy"],
n_range=[10 ** k for k in range(1, 9)],
)
ms = 10
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1)
plt.loglog(
out.n_range,
out.n_range * np.log(out.n_range) * 1.0e-8,
"o-",
label="$c \; n \; log(n)$",
)
plt.loglog(out.n_range, out.timings[0] * 1.0e-9, "o-", ms=ms, label="Cython")
plt.loglog(out.n_range, out.timings[1] * 1.0e-9, "o-", ms=ms, label="Numba")
plt.loglog(out.n_range, out.timings[2] * 1.0e-9, "o-", ms=ms, label="NumPy")
markers = iter(["", "o", "v", "^"])
for i, line in enumerate(ax.get_lines()):
marker = next(markers)
line.set_marker(marker)
plt.legend()
plt.grid("on")
_ = ax.set_ylabel("Runtime [s]")
_ = ax.set_xlabel("n = len(A)")
_ = ax.set_title("Timings of merge sort")
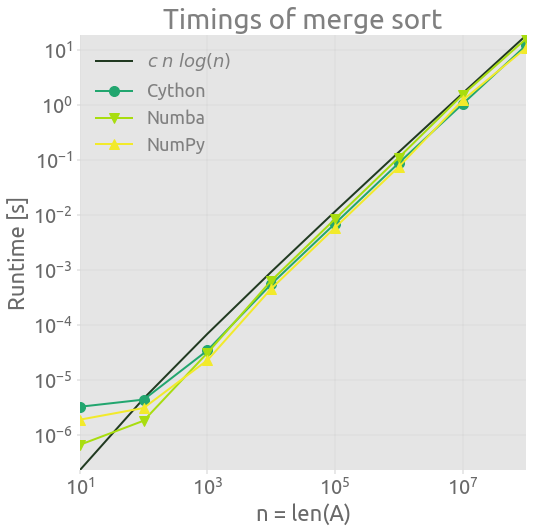
Conclusion
Numba is really easy to use. When dealing with NumPy arrays, it is impressive that it can perform as well as efficient C or Cython just by adding a simple decorator to a Python function.