A Cython implementation of a priority queue

abstract_data_structure

Credit: Musée de l'illusion, Lyon (picture taken by myself)

In this post, we describe a basic Cython implementation of a priority queue.

A priority queue is an important data structure in computer science with many applications. In the present post, our motivation is to write a priority queue for classic shortest path algorithms, such as Dijkstra’s Single Source Shortest Path (SSSP). We target rather sparse graphs, such as transportation networks.

The Priority queue operations

For that kind of algorithms, we have a fixed set of elements, usually either the graph vertices or edges, each associated with a key real number. This key value may represent a travel time from an origin, for example. The purpose of the priority queue is to be able to extract the element from the queue with minimum priority key. Also, we need to be able to insert some elements with a given key into the queue, and to decrease the key of an element from the queue. This happens for example in SSSP when a shorter path to a vertex is found.

As described by Chen in [1]:

A priority queue is a collection of elements each with a numerical priority, also known as its key. Priority queues support insert, extract-min operations. An insert operation adds one element and its key into the priority queue. A call to extract-min deletes the element with the lowest key from the queue, and returns the element with its key.
Optionally, a priority queue may support delete and decrease-key operation. The decrease-key operation takes as its parameters an element reference, and a new key. The result is that if the element is present in the priority queue, its current key is replaced with the new key. To implement delete and decrease-key operations efficiently, a priority queue must be able to access specific elements in constant time. Usually this is done by keeping a table of element pointers.

In the present case, we are going to implement the decrease-key operation, not the delete one. So we are going to need a table of “element pointers”, which implies some kind of heavy mechanism. However, we are only going to deal with indices and not direct memory location addresses. This will be described in a following section. Note that it is possible to implement the SSSP algorithm without the decrease-key operation in the priority queue, but we need this operation for other algorithms than SSSP.

To summarize, we are going to build a data structure for maintaining a set $S$ of elements, each with an associated value called a key, and supporting the following operations:

INSERT($S$, $x$, $k$) inserts the element $x$ with key $k$ into the set $S$
EXTRACT-MIN($S$) removes and returns the element of $S$ with the smallest key.
DECREASE-KEY($S$, $x$, $k$) decreases the value of element $x$’s key to the new value $k$, which is assumed to be at most as large as $x$’s current key value.

The above notations are take from Cormen et al. [2].

The Underlying heap

There are many possible implementations of this data structure. It is possible to base a priority queue on a linked list. However, when the network is rather sparse, using a priority queue based on a heap is more efficient. Several heap types can be used for a priority queue, for example Binary, Binomial or Fibonacci heaps. The Fibonacci heap has a better theoretical time complexity than the binary heap, but it is not so clear in practice : constant factors may differ a lot from one heap type to another. As explained by Delling et al. in [3]:

However, in practice the impact of priority queues on performance for large road networks is rather limited since cache faults for accessing the graph are usually the main bottleneck. In addition, our experiments indicate that the impact of priority queue implementations diminishes with advanced speedup techniques that dramatically reduce the queue sizes.

It is also possible to exploit the property that the sequence of values returned by the EXTRACT-MIN calls in Dijkstra’s algorithm are monotonically increasing over time, as mentioned in [2]:

in this case several data structures can implement the various priority-queue operations more efficiently than a binary heap or a Fibonacci heap.

In our implementation, we are going to keep the code as simple as possible and use the most rudimentary heap type: a binary heap, that does not take advantage of this monotone property. Note that we already used such a data structure, for the purpose of sorting, in previous posts:

We refer to the first of these two posts for a description of a binary heap.

The Data containers

We base our implementation on an implicit approach, as described by Larkin et al. [4]:

The tree can be stored explicitly using heap-allocated nodes and pointers, or it can be encoded implicitly as a level-order traversal in an array. We refer to these variations as explicit and implicit heaps respectively. The implicit heap carries a small caveat, such that in order to support DecreaseKey efficiently, we must rely on a level of indirection: encoding the tree’s structure as an array of node pointers and storing the current index of a node’s pointer in the node itself […].

So we are going to deal with two arrays:

an array of structs for the elements
an array of indices for the binary tree

The shortest path algorithm deals with a set of $n$ elements, e.g. $n=|V|$ where $V$ are the graph vertices. We store these elements in a first array:

element_array

In a second array, we store an array-based binary tree:

tree_array

In the following, we denote by A the binary tree array and Elements the element array. A is an implicit data structure. Given a node index i, the parent node index can be easily found as (i - 1) // 2. The left child has index 2 * i + 1 and the right child 2 * (i + 1). The root is located at index 0.

Heap length

The length of the tree array could be smaller than the element array because the heap size is usually much smaller that the total number of elements $n$, especially for sparse graphs. However, in the present post, we keep a tree array of the same length as the elements array, $n$, in order to guarantee that all the elements fit in the heap.

Mutual references

The path algorithm is only dealing with the elements, which are stored in the element array, and call the priority queue operations: insert, extract-min and decrease-key. The order of the elements in the element array is never changed, while items in the binary tree are permuted, in order to meet the min-heap property: a value of a given node i is not smaller than the value of its parent node parent(i).

So we need some kind of mutual references, in order to associate an element in the heap to a tree node, and vice-versa. Since we have an array storing the elements, we are going to use indices to refer to the associated tree nodes. As Robert Sedgewick explains in [5]:

Suppose that the records to be processed in a priority queue are in an existing array. In this case, it makes sense to have the priority-queue routines refer to items through the array index. Moreover, we can use the array index as a handle to implement all the priority-queue operations.

So there is a node_idx attribute in Elements, referring to some binary tree node. Conversely, we are also going to store the element_idx in A. The key value is stored in the Element array.

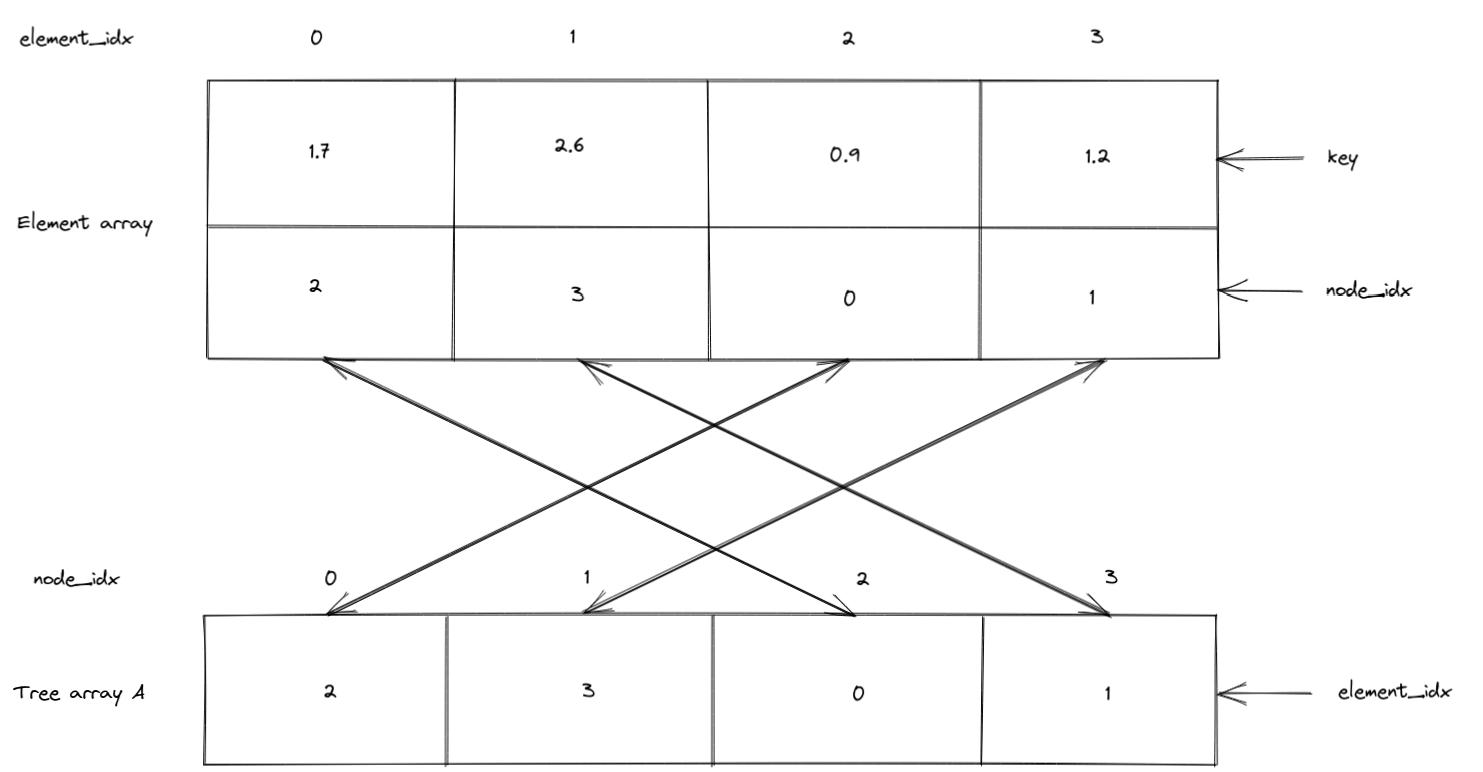
mutual_refs

We have the following invariants:

Elements[A[i]].node_idx = i

and

A[Elements[i].node_idx] = i.

And the min-heap property can be stated as follows:

Elements[A[parent(i)]].key <= Elements[A[i]].key

Element state

One last thing is required: the element state. Since the heap size vary, elements may be or not in the heap. All the elements from the heap can be found in the size first elements of the tree array A: the A[0] to A[size-1] tree nodes correspond to elements in the heap, while the A[size] to A[n] tree nodes are not in the heap.

Path algorithms only deal with elements, not tree nodes, which belong to some kind of internal mechanism. There is a possibility that path algorithms, on the higher level, try to insert into the heap an element that was already popped from it. This is useless, since a shortest path may already exist for this element. So we need some kind of state flag to know if an element has already been scanned or not. We also use this state flag to check if an element is in the heap or not, which is more convenient than checking if the associated node index is smaller than the heap size. So we have 3 distinct states:

SCANNED
NOT_IN_HEAP
IN_HEAP

Elements are initialized as NOT_IN_HEAP, with an inf key value and a node_idx equal to the heap length. The tree array is initialized with a element_idx also equal to the number of elements, which happens to be the heap length in our implementation.

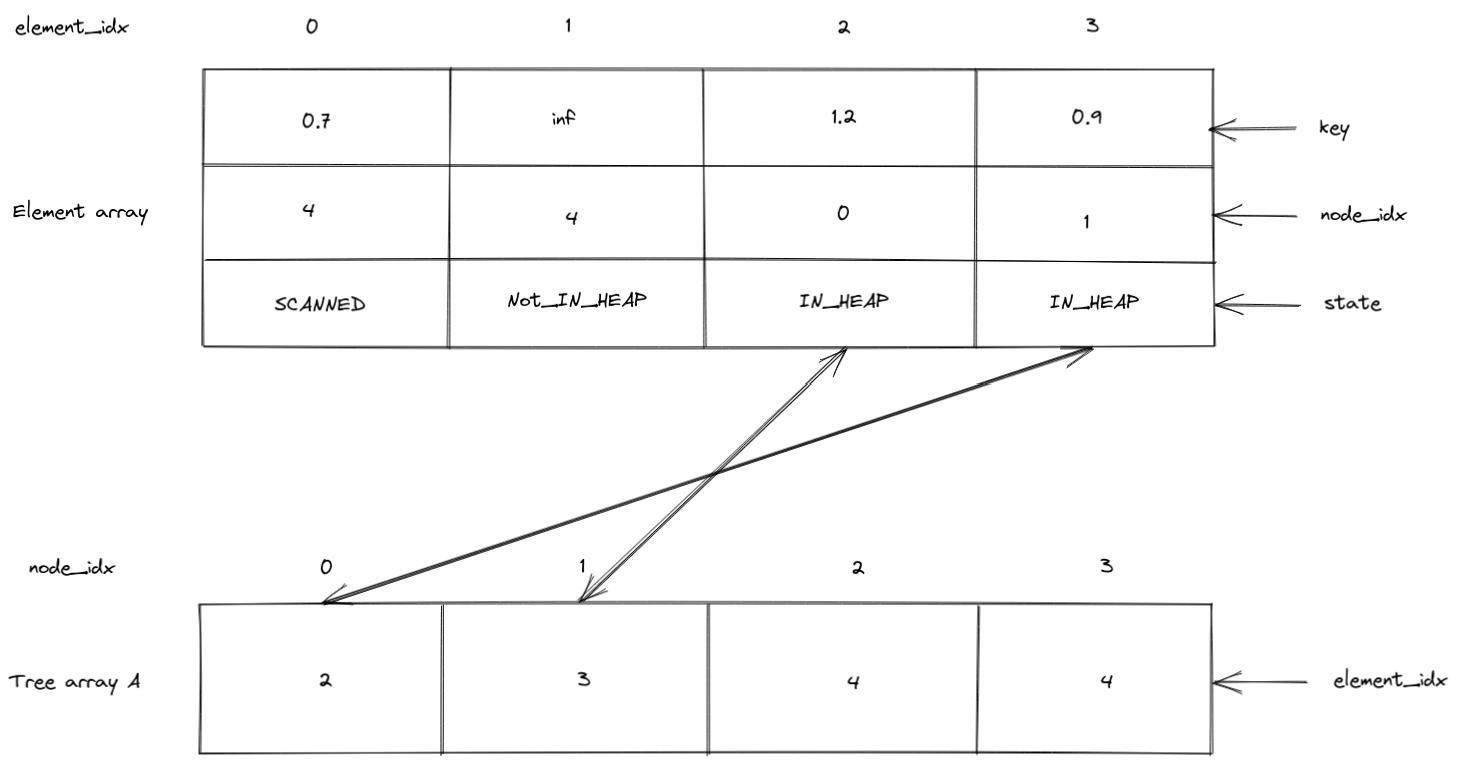
mutual_refs

Imports

%load_ext cython

Package versions:

Python version       : 3.10.7
cython               : 0.29.32
jupyterlab           : 3.5.0
numpy                : 1.23.5

Cython code

Remarks:

The key data type is defined as float64
We define an “infinity” as the maximum value that that can be store in the key data type. This is used to initialize the key value.
We use an enumeration for the element state to associate the state name with an integer and make it easier to read
Indices are defined as size_t
The GIL is released in all the functions
This priority queue code can only be called from some Cython code
We wrote a very small toy test at the end, that can be called from a Python cell

%%cython --compile-args=-Ofast
# cython: language_level=3, boundscheck=False, wraparound=False, embedsignature=False, initializedcheck=False
# distutils: define_macros=NPY_NO_DEPRECATED_API=NPY_1_7_API_VERSION

import numpy as np

cimport numpy as cnp
from libc.stdlib cimport free, malloc

# data type for the key value
ctypedef cnp.float64_t DTYPE_t
cdef DTYPE_t DTYPE_INF = <DTYPE_t>np.finfo(dtype=np.float64).max

cdef enum ElementState:
   SCANNED      # popped from the heap
   NOT_IN_HEAP  # never been in the heap
   IN_HEAP      # in the heap

cdef struct Element:
    ElementState state # element state wrt the heap
    size_t node_idx   # index of the corresponding node in the tree
    DTYPE_t key        # key value

cdef struct PriorityQueue:
    size_t  length    # maximum heap size
    size_t  size      # number of elements in the heap
    size_t* A         # array storing the binary tree
    Element* Elements  # array storing the elements

cdef void init_pqueue(
    PriorityQueue* pqueue,
    size_t length) nogil:
    """Initialize the priority queue.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t length : length (maximum size) of the heap
    """
    cdef size_t i

    pqueue.length = length
    pqueue.size = 0
    pqueue.A = <size_t*> malloc(length * sizeof(size_t))
    pqueue.Elements = <Element*> malloc(length * sizeof(Element))

    for i in range(length):
        pqueue.A[i] = length
        _initialize_element(pqueue, i)

cdef inline void _initialize_element(
    PriorityQueue* pqueue,
    size_t element_idx) nogil:
    """Initialize a single element.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t element_idx : index of the element in the element array
    """
    pqueue.Elements[element_idx].key = DTYPE_INF
    pqueue.Elements[element_idx].state = NOT_IN_HEAP
    pqueue.Elements[element_idx].node_idx = pqueue.length

cdef void free_pqueue(
    PriorityQueue* pqueue) nogil:
    """Free the priority queue.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    """
    free(pqueue.A)
    free(pqueue.Elements)

cdef void insert(
    PriorityQueue* pqueue,
    size_t element_idx,
    DTYPE_t key) nogil:
    """Insert an element into the priority queue and reorder the heap.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t element_idx : index of the element in the element array
    * DTYPE_t key : key value of the element

    assumptions
    ===========
    * the element pqueue.Elements[element_idx] is not in the heap
    * its new key is smaller than DTYPE_INF
    """
    cdef size_t node_idx = pqueue.size

    pqueue.size += 1
    pqueue.Elements[element_idx].state = IN_HEAP
    pqueue.Elements[element_idx].node_idx = node_idx
    pqueue.A[node_idx] = element_idx
    _decrease_key_from_node_index(pqueue, node_idx, key)

cdef void decrease_key(
    PriorityQueue* pqueue,
    size_t element_idx, 
    DTYPE_t key_new) nogil:
    """Decrease the key of a element in the priority queue, 
    given its element index.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t element_idx : index of the element in the element array
    * DTYPE_t key_new : new value of the element key 

    assumption
    ==========
    * pqueue.Elements[idx] is in the heap
    """
    _decrease_key_from_node_index(
        pqueue, 
        pqueue.Elements[element_idx].node_idx, 
        key_new)

cdef size_t extract_min(PriorityQueue* pqueue) nogil:
    """Extract element with min key from the priority queue, 
    and return its element index.

    input
    =====
    * PriorityQueue* pqueue : priority queue

    output
    ======
    * size_t : element index with min key

    assumption
    ==========
    * pqueue.size > 0
    """
    cdef: 
        size_t element_idx = pqueue.A[0]  # min element index
        size_t node_idx = pqueue.size - 1  # last leaf node index

    # exchange the root node with the last leaf node
    _exchange_nodes(pqueue, 0, node_idx)

    # remove this element from the heap
    pqueue.Elements[element_idx].state = SCANNED
    pqueue.Elements[element_idx].node_idx = pqueue.length
    pqueue.A[node_idx] = pqueue.length
    pqueue.size -= 1

    # reorder the tree elements from the root node
    _min_heapify(pqueue, 0)

    return element_idx

cdef inline void _exchange_nodes(
    PriorityQueue* pqueue, 
    size_t node_i,
    size_t node_j) nogil:
    """Exchange two nodes in the heap.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t node_i: first node index
    * size_t node_j: second node index
    """
    cdef: 
        size_t element_i = pqueue.A[node_i]
        size_t element_j = pqueue.A[node_j]
    
    # exchange element indices in the heap array
    pqueue.A[node_i] = element_j
    pqueue.A[node_j] = element_i

    # exchange node indices in the element array
    pqueue.Elements[element_j].node_idx = node_i
    pqueue.Elements[element_i].node_idx = node_j

    
cdef inline void _min_heapify(
    PriorityQueue* pqueue,
    size_t node_idx) nogil:
    """Re-order sub-tree under a given node (given its node index) 
    until it satisfies the heap property.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t node_idx : node index
    """
    cdef: 
        size_t l, r, i = node_idx, s

    while True:

        l =  2 * i + 1  
        r = l + 1
        
        if (
            (l < pqueue.size) and 
            (pqueue.Elements[pqueue.A[l]].key < pqueue.Elements[pqueue.A[i]].key)
        ):
            s = l
        else:
            s = i

        if (
            (r < pqueue.size) and 
            (pqueue.Elements[pqueue.A[r]].key < pqueue.Elements[pqueue.A[s]].key)
        ):
            s = r

        if s != i:
            _exchange_nodes(pqueue, i, s)
            i = s
        else:
            break
    
cdef inline void _decrease_key_from_node_index(
    PriorityQueue* pqueue,
    size_t node_idx, 
    DTYPE_t key_new) nogil:
    """Decrease the key of an element in the priority queue, given its tree index.

    input
    =====
    * PriorityQueue* pqueue : priority queue
    * size_t node_idx : node index
    * DTYPE_t key_new : new key value

    assumptions
    ===========
    * pqueue.elements[pqueue.A[node_idx]] is in the heap (node_idx < pqueue.size)
    * key_new < pqueue.elements[pqueue.A[node_idx]].key
    """
    cdef:
        size_t i = node_idx, j
        DTYPE_t key_j

    pqueue.Elements[pqueue.A[i]].key = key_new
    while i > 0: 
        j = (i - 1) // 2  
        key_j = pqueue.Elements[pqueue.A[j]].key
        if key_j > key_new:
            _exchange_nodes(pqueue, i, j)
            i = j
        else:
            break


# Simple example
# ==============

cpdef test_01():

    cdef PriorityQueue pqueue

    init_pqueue(&pqueue, 4)

    insert(&pqueue, 1, 3.0)
    insert(&pqueue, 0, 2.0)
    insert(&pqueue, 3, 4.0)
    insert(&pqueue, 2, 1.0)

    assert pqueue.size == 4
    A_ref = [2, 0, 3, 1]
    n_ref = [1, 3, 0, 2]
    key_ref = [2.0, 3.0, 1.0, 4.0]
    for i in range(4):
        assert pqueue.A[i] == A_ref[i]
        assert pqueue.Elements[i].node_idx == n_ref[i]
        assert pqueue.Elements[i].state == IN_HEAP
        assert pqueue.Elements[i].key == key_ref[i]

    decrease_key(&pqueue, 3, 0.0)

    assert pqueue.size == 4
    A_ref = [3, 0, 2, 1]
    n_ref = [1, 3, 2, 0]
    key_ref = [2.0, 3.0, 1.0, 0.0]
    for i in range(4):
        assert pqueue.A[i] == A_ref[i]
        assert pqueue.Elements[i].node_idx == n_ref[i]
        assert pqueue.Elements[i].state == IN_HEAP
        assert pqueue.Elements[i].key == key_ref[i]
    
    element_idx = extract_min(&pqueue)
    assert element_idx == 3

    free_pqueue(&pqueue)

test_01()

Everything seems to work fine. In a future post, we will use this priority queue in a shortest path algorithm, and try to measure its efficiency.

References

[1] Chen, M., Measuring and Improving the Performance of Cache-efficient Priority Queues in Dijkstra’s Algorithm, 2007.
[2] Cormen et al., Introduction to Algorithms, MIT Press and McGraw-Hill, coll. « third », 2009.
[3] Delling et al., Engineering Route Planning Algorithms. In: Lerner, J., Wagner, D., Zweig, K.A. (eds) Algorithmics of Large and Complex Networks. Lecture Notes in Computer Science, vol 5515. Springer, Berlin, Heidelberg, 2009. https://doi.org/10.1007/978-3-642-02094-0_7
[4] Larkin et al., A back-to-basics empirical study of priority queues. In Proceedings of the 16th Workshop on Algorithm Engineering and Experiments (ALENEX), pages 61–72, 2014.
[5] Robert Sedgewick. Algorithms in C (3rd. ed.). Addison-Wesley Longman Publishing Co., Inc., USA, 2002.